Información y Entropía (NOTA 1)
Guillermo Agudelo Murguía
José Guillermo Alcalá Rivero
Introducción
Para poder establecer la dialéctica de una conversación científica, en primer lugar es necesario demarcar los campos semánticos de los conceptos utilizados. Es sabido que uno de los problemas que existe en el estudio científico de las humanidades es la necesidad que se tiene de emplear términos de uso común, en tanto que las ciencias duras crean su propia terminología, aceptada o no por la Academia de la lengua. Es así que a conceptos como Información, Conocimiento, Complejidad, etc. se les deben asignar definiciones aceptadas por los participantes en el diálogo, debido a la tremenda carga connotativa que conllevan. Por ejemplo ¿qué se entiende por realidad? Este concepto, obviamente, es muy difícil de definir. Si se intentara darle una definición en un grupo, cada integrante del mismo, muy probablemente, aportaría una versión propia. Sin embargo, creemos que el término se debe relativizar en cuanto al tiempo, cultura, estrato social, etc. Así, la realidad es una y muy diferente para una cultura occidental de la Ilustración que para la sociedad comunista rusa del siglo XX o para la sociedad neoliberal del siglo XXI. E inclusive, la realidad dentro de esta sociedad neoliberal se diferencia entre el estrato social de las clases dominantes y las dominadas, con una serie de matices muy marcados.
Por otro lado, un concepto como adaptabilidad requiere de una definición más completa. Es cierto que la adaptabilidad significa, en ciertos casos, incremento de complejidad, pero, también puede significar una pérdida de la misma. En oposición a los sistemas complejos adaptables (SCA), los sistemas complejos evolutivos (SCE) no pierden complejidad, sólo la incrementan. Por otro lado podemos hablar de la adaptabilidad en cuanto al grado de libertad que el ser humano tiene para, erróneamente, tratar de que la naturaleza se adapte a su hedonismo y no la co-adaptación que la naturaleza demanda de los sistemas que la integran, ser humano incluido.
La adaptabilidad es en sí un fenómeno mucho más aceptado por la facilidad que se tiene de observarlo en lapsos de tiempo mucho más asequibles al ser humano e inclusive de interferir directamente en él. (Recuérdese el caso de las razas de perros palomas, híbridos vegetales y animales, etc.) En tanto que requeriría miles de millones de años el observar todo el proceso de un SCE, como una estrella, que pega el salto evolutivo y adquiere planetas. Por otro lado, considérese el caso del híbrido de un yegua y asno, esto es simplemente una adaptación, para que pudiera darse el salto evolutivo se necesitaría que los dos sistemas progenitores desaparecieran como tales y se integraran en un nuevo sistema.
Posiblemente Bekenstein en su artículo La información en el universo holográfico (NOTA 2) no enuncia una definición explicita de Información. Sin embargo a lo largo de su artículo el autor da los elementos suficientes para formar una definición de este concepto que esté de acuerdo con los lineamientos de la lógica formal.
Concepto definido:
La Información
Clase general a la que pertenece el concepto:
Elemento del mundo físico de la misma importancia que “materia y energía”.
Características generales que la identifican:
-
Son las instrucciones suficientes para que elementos o sistemas cumplan sus funciones. Ejemplos: El robot de una fábrica de automóviles es de metal y plástico, pero no hará nada útil sin abundantes instrucciones que le digan que pieza ha de soldar a otra. Una ribosoma de una célula se construye de aminoácidos y se alimenta con la energía generada por la conversión del ATP en ADP, pero no podría sintetizar proteínas sin la información suministrada por el ADN del núcleo celular.
-
Desempeña una función esencial en los sistemas y procesos físicos
John a. Wheeler, de la Universidad de Princeton, considera que el mundo físico está hecho de información; la energía y la materia serían accesorios.
Por otro lado, en el ensayo Mente – Cuerpo (Agudelo, Alcalá, 2003), los autores proponen lo siguiente:
La Información en la Vida esta integrada a la energía-materia y se recibe en forma de instrucciones endógenas y exógenas, materiales e inmateriales (como fotones, por ejemplo) que se guardan en la memoria, en capas temporales relacionadas con las capas cerebrales y de acuerdo con cada subsistema del organismo. La Información le proporciona a los sistemas la característica ejecutiva que les permite obedecer de manera determinista o seleccionar su respuesta de un rango de posibilidades, según sus grados de libertad. De acuerdo con Shannon (entropía de la información) y Boltzmann (entropía termodinámica), nosotros proponemos que la medida de la información más ampliamente usada hoy en día es la entropía.
Las dos entropías
La teoría formal de la información nació de los artículos publicados en 1948 por el matemático estadounidense Claude E. Shannon. En ellos enunció: la medida de la información más ampliamente usada hoy en día es la entropía. La entropía había venido siendo un concepto central de la termodinámica, la rama de la física que trata del calor. Suele decirse que la entropía termodinámica expresa el desorden de un sistema físico. En 1877 el físico austriaco Ludwig Boltzmann la caracterizó más precisamente como el número de estados microscópicos distintos en los que pueden hallarse las partículas que componen un trozo de materia de forma que siga pareciendo el mismo trozo desde un punto de vista macroscópico. En el caso del aire de una habitación, se contarían las maneras en que podrían distribuirse y moverse las moléculas de gas por la habitación.
Claro que esta conceptualización de Boltzmann va muy de acuerdo con la idea de que la suma de las partes aisladas no da como resultado el todo. Actualmente se acepta que a la suma de las partes debe agregársele los valores de las interacciones de estas partes, las ligas que contienen la Información que determina su comportamiento.
Cuando Shannon buscó una manera de cuantificar la información contenida en un mensaje, la lógica le condujo a una fórmula que tenía el mismo aspecto que la de Boltzmann. La entropía de Shannon de un mensaje es el número dígitos binarios, o bits, necesarios para codificarlo. Aunque no nos ilustra acerca del valor de la información, que depende mucho del contexto; en cuanto medida objetiva de la cantidad de información, la entropía de Shannon ha sido enormemente útil en ciencia y técnica. El diseño de todos los aparatos modernos de comunicación –desde los teléfonos portátiles hasta los módems y los reproductores de discos compactos-- se basa en la entropía de Shannon.
La entropía termodinámica y la de Shannon son conceptualmente equivalentes: el número de configuraciones que se cuentan en la entropía de Boltzmann refleja la cantidad de información de Shannon que se necesitaría para realizar cualquier configuración determinada. Tales entropías presentan, sin embargo, dos diferencias principales. En primer lugar, la entropía termodinámica que emplea un químico o un experto en refrigeración se expresa en unidades de energía dividida por temperatura, mientras que la entropía de Shannon aplicada por un ingeniero de telecomunicaciones se da en bits, magnitud que carece de dimensión. Esta diferencia no es más que una cuestión de convenciones.
Incluso cuando se les ha reducido a unidades comunes, los valores típicos de las dos entropías difieren mucho en magnitud. Un microchip de silicio que contenga un gigabyte de datos, por ejemplo, posee una entropía de Shannon de unos 1010 bits (un byte son ocho bits), muchísimo menor que la entropía termodinámica del chip, unos 1023 bits a temperatura ambiente. Esta discrepancia se debe a que esas entropías se calculan para grados de libertad diferentes. Un grado de libertad es cualquier cantidad que pueda cambiar, así una coordenada que especifica la localización de una partícula o una componente de su velocidad. La entropía de Shannon del chip sólo atiende al estado global de cada pequeño transistor impreso en el cristal de silicio: está on u off; representa un 0 o un 1 –un único grado de libertad binario--. La entropía termodinámica, por el contrario depende de los estados de todos y cada uno de los miles de millones de átomos (con sus electrones en órbita) que forman cada transistor. A medida que la miniaturización nos acerque más al día en que cada átomo nos almacenará un bit de información, la entropía útil de Shannon del mejor microchip del momento se ira acercando a la entropía termodinámica de su materia. Cuando las dos entropías se calculan para los mismos grados de libertad, resultan iguales.
¿Cuáles son los grados de libertad fundamentales? Después de todo, los átomos se componen de electrones y núcleos, los núcleos de protones y neutrones, y éstos de quarks. Muchos consideran hoy en día que los electrones y los quarks son excitaciones de supercuerdas, de las que piensan que son entes más fundamentales. Pero las vicisitudes de un siglo de revelaciones en la física nos previenen contra el dogmatismo. Podría haber más niveles de estructura en nuestro universo que los que sueña la física actual.
No se puede calcular la capacidad máxima de información de un pedazo de materia, o, de manera equivalente, su verdadera entropía termodinámica, sin conocer la naturaleza de los últimos constituyentes de la materia o del nivel más profundo de la estructura, al que llamaré “nivel X”. (Esta ambigüedad no le causa problemas en el análisis de la termodinámica práctica, por ejemplo, la de un motor de coche, ya que se puede ignorar los quarks del interior del átomo; ellos no cambian de estado bajo las condiciones relativamente moderadas del motor.) Dado el vertiginoso progreso de la miniaturización, juguemos a imaginar un día en que los quarks sirviesen para almacenar información, quizás un bit cada uno. ¿Cuánta información cabría entonces en nuestro cubo de un centímetro de lado? ¿Y cuánta si lográsemos controlar la supercuerda, o niveles más profundos aún ni soñados? Sorprendentemente, los desarrollos de la física de la gravitación en los treinta últimos años han proporcionado algunas respuestas claras a preguntas que parecían inabordables.
Algo que no considera Shannon es la información que el chip en sí ya contiene, la que lo capacita para recibir la información del mensaje. Es así que la afirmación de que “Cuando las dos entropías sean calculadas con base en los mismos grados de libertad, su resultado será igual” es obvia. Es imposible para un quark aceptar información adicional, ya que perdería su calidad de quark al tener que aceptar, además de la información que ya contiene, la información de un mensaje o instrucción adicional.
La pregunta que sigue sería: ¿las cuerdas son en sí la información “inmaterial” o son estructuras “materiales” que forman el quark? De ser estructuras “materiales”, estas cuerdas deben contener la información que las conduzca a constituir el quark. Esto nos lleva a pensar que en el dilema de que está constituida la esencia del universo: materia o información, nuestra respuesta sería: ambas
La Información termodinámica de la cual la entropía nos da su medida sólo se refiere al sistema inmediato en el que actúa. Así, las partes que integran un escritorio tienen valor como tal si se posee la información que permite armarlo. Las partes del cajón del escritorio, sólo nos dan la Información sobre el cajón, no la suficiente sobre el escritorio.
Por otro lado, el ejemplo deja claro que la información que se obtiene por la entropía de Shannon es mucho menor que la entropía termodinámica de Boltzmann porque de esta última se puede obtener la Información contenida a niveles más profundos de las estructuras que forman el chip, en tanto que la entropía de Shannon da la Información del chip como estructura básica. La diferencia entre 1010 bits y 1023 bits es la información necesaria para construir el chip a partir de los elementos más finos logrados.
Sin embargo, tenemos que aceptar que la tesis que sostenemos que la Información es la base de la emergencia y evolución del universo no es nueva. En el libro The Mind and the Brain (NOTA 3), los autores afirman que tanto los legos como los científicos consideran que el mundo está construido por diminutos fragmentos de materia, esto va de acuerdo con la visión de la ciencia ortodoxa reduccionista, que estudia de la parte al todo, pero ellos señalan que esta visión es incorrecta. Ya en 1930, el matemático húngaro John von Neumann propuso una versión de la teoría cuántica, en la que postula que “el mundo no esta construido por fragmentos de materia sino por fragmentos de conocimiento…” Sin embargo, reconocen que esta idea se perdió rápidamente cuando el materialismo surgió triunfante, el cual a pesar de haberse impuesto ha sido incapaz de explicar como emerge la Información.
La información y los agujeros negros
Si preguntamos de que se compone el mundo físico, se nos responderá que de “materia y energía”. Pero quien sepa algo de ingeniería, biología y física nos citará también la información como elemento no menos importante…Un siglo de investigación nos ha enseñado que la información desempeña una función esencial en los sistemas y procesos físicos. Hoy, una líneas de pensamiento iniciada por John A. Wheeler de la Universidad de Princeston considera que el mundo físico está hecho de información; la energía y la materia serían accesorios.
Estimamos que la información está siempre integrada con la materia- energía no pueden existir separados. De hecho, creemos, de acuerdo con el Principio de Zeilinger, que el elemento fundamental del universo es ya un sistema elemental formado por un bit y la energía que lo contiene.
Este punto de vista invita a reconsiderar cuestiones fundamentales. La capacidad de almacenamiento de la información de los discos duros y demás dispositivos de memoria ha ido creciendo a toda velocidad. ¿Cuándo se parará este progreso? ¿Cuál es la capacidad de información última de un dispositivo que pese, digamos, menos de un gramo y ocupe un centímetro cúbico (ése viene a ser el tamaño del chip de un ordenador)? ¿Cuánta información se necesita para describir todo un universo? ¿Podría tal descripción caber en la memoria de un ordenador? ¿Podríamos, tal como escribió William Blake, “ver el mundo en un grano de arena”, o esas palabras sólo han de tomarse como una licencia poética?
Desarrollos recientes de la física teórica contestan algunas de estas preguntas; las respuestas podrían ser hitos importantes hacia la teoría definitiva de la realidad (El llegar a la realidad definitiva como lo dice el autor significaría el obtener la respuesta a la última pregunta, lo que a su vez significaría llegar al Conocimiento absoluto, alguien diría a Dios mismo). Del estudio de las misteriosas propiedades de los agujeros negros se han deducido límites absolutos que acotan la información que cabe en una región del espacio o en una cantidad de materia y energía…
La termodinámica del agujero negro
Protagonista de estos avances es el agujero negro. Los agujeros negros son una consecuencia de la relatividad general, teoría geométrica de la gravitación establecida por Albert Einstein en 1915. Según esta teoría, la gravitación surge de la curvatura del espacio-tiempo, que hace que los objetos se muevan como si fuesen atraídos por una fuerza. A la inversa, la curvatura es causada por la presencia de materia y energía. Es así que para nosotros esta presencia de materia y energía le informa al espacio como curvarse, a su vez, la curvatura interacciona informándole a la materia como debe moverse.
Según las ecuaciones de Einstein, una concentración suficientemente densa de materia o energía curvará el espacio-tiempo tan extremadamente que lo rasgará y nacerá un agujero negro. Las leyes de la relatividad prohíben a todo lo que caiga en un agujero negro volver a salir; por lo menos dentro de la formulación clásica (es decir, no cuántica), de la física. El punto de no retorno, llamado el evento de horizonte del agujero negro es de crucial importancia. En el caso más simple, el horizonte es una esfera cuya área superficial es mayor cuanto mayor sea la masa del agujero negro.
Es imposible determinar lo que hay dentro de un agujero negro. Ninguna información detallada puede emerger del horizonte y escapar al mundo exterior. Al desaparecer para siempre en un agujero negro, la materia deja algunos rastros. Su energía (contamos cualquier masa como energía, de acuerdo con la fórmula de Einstein E = mc2) queda permanentemente reflejada en un incremento de la masa del agujero negro. Si la materia es capturada al orbitar el hoyo, su momento angular correspondiente se agrega al momento angular del agujero negro. Tanto la masa como el momento angular del agujero negro son mensurables gracias a sus efectos en el espacio-tiempo de los alrededores del agujero; así, los agujeros negros respetan las leyes de conservación de la energía y del momento angular. Otra ley fundamental, la segunda ley de la termodinámica parece ser violada.
La segunda ley de la termodinámica compendia algo conocido por todos: que la mayoría de los procesos naturales son irreversibles. Una taza de té cae de la mesa y se rompe; nadie ha visto jamás que los trozos salten del suelo y recompongan la taza. La segunda ley de la termodinámica prohíbe la inversión del proceso. Establece que la entropía de un sistema físico aislado nunca decrece; en el mejor de los casos, permanecerá constante; por lo normal, aumentará. Esta ley es esencial para la físico-química y la ingeniería; cabe sostener que es la ley física que más impacto ha causado fuera de la física.
Como lo enfatizó Wheeler, cuando la materia desaparece en un agujero negro desaparece también su entropía y parece que la segunda ley es trascendida, pierde su relevancia. Una idea de cómo podría resolverse este problema llegó en 1970. Demetrious Chritodoulou, entonces estudiante de doctorado de Wheeler en Princeton, y por otra parte Stephen W. Hawking, de la universidad de Cambridge, demostraron que en varios procesos, entre ellos la fusión de dos agujeros negros, nunca decrecía el área total de los horizontes de sucesos. La analogía con la tendencia de la entropía a aumentar me llevó a proponer en 1972 que un agujero negro tiene una entropía proporcional al área de su horizonte (véase la figura 1). Conjeturé que, cuando la materia cae en un agujero negro, el aumento de la entropía de éste siempre compensa, con creces incluso, la entropía “perdida” por la materia. Más generalmente, la suma de la entropía del agujero negro y de la entropía ordinaria fuera del mismo no puede decrecer. Esta es la generalización de la segunda ley (o GSL).
La GSL ha superado un gran número de estrictas pruebas, si bien puramente teóricas. Cuando una estrella se desploma sobre sí misma y crea un agujero negro, la entropía de éste supera en mucho la de la estrella (esto quiere decir que el agujero negro incrementa su información). En 1974 Hawking demostró que un agujero negro emite espontáneamente radiaciones térmicas mediante un proceso cuántico, hoy denominada “radiación de Hawking”. El teorema de Christodoulou-Hawking falla ante ese fenómeno (la masa del agujero negro y, por tanto, el área de su horizonte decrecen), pero la GSL resuelve el problema: la entropía de la radiación emergente compensa la merma de la entropía del agujero negro, de manera que se conserva la GSL. En 1986 Rafael D. Sorkin, de la universidad de Syracuse, utilizó la función del horizonte como bloqueador de la información interna del agujero que impide que influya en el exterior, para demostrar que la GSL (o algo muy parecido a ella) tiene que ser válido en cualquier proceso concebible que sufran los agujeros negros. Su profundo argumento dejaba claro que la entropía a que se refiere la GSL coincide con la calculada en el nivel X, sea cual sea ese nivel. Esto nos hace inferir que el agujero negro puede llegar a obtener la entropía total, es decir, transformar todo en Información.
Con su proyecto de radiación Hawkings determinó la constante de proporcionalidad entre la entropía de un agujero negro y el área del horizonte: la entropía del agujero negro es exactamente una cuarta parte del área del horizonte de eventos medida en áreas de Planck. (La longitud de Planck, unos 10-33 centímetros es la escala de longitud fundamental relacionada con la gravedad y la mecánica cuántica. El área de Planck es un cuadrado). Incluso, desde un punto de vista termodinámico, se trata de una enorme cantidad de entropía. La entropía de un agujero negro de un centímetro de diámetro sería de unos 1066 bits, aproximadamente igual a la entropía termodinámica de un cubo de agua de 10.000 millones de kilómetros de lado.
Leonard Susskind y ‘t Hooft (NOTA 4) argumentan que la Información que contiene la materia que es absorbida por un agujero negro es recuperable, en oposición a lo enunciado por Hawking en el sentido de que nada de lo que cae en un agujero negro es recuperable (NOTA 5). Para este último la información codificada en sus átomos constituyentes es irrecuperable. Sin embargo ‘t Hooft señala que si esa información realmente se perdiera la mecánica cuántica colapsaría. A pesar de su famosa ley de la indeterminación, la mecánica cuántica controla el comportamiento de las partículas en una forma muy específica: Su reversibilidad. Al interactuar una partícula con otra se absorbe, se refleja o se descompone en otras partículas. Pero uno siempre puede reconstruir las configuraciones iniciales de las partículas, de los productos finales. Si esta regla es violada por los agujeros negros la energía puede ser creada o destruida. Esto amenaza una de los más esenciales fundamentos de la física.
A lo largo del tiempo un hoyo negro aislado radia toda su masa antes de desvanecerse. La consistencia de la mecánica cuántica requiere que esta energía radiada se lleve también toda la Información.
Llegamos a las siguientes conclusiones:
-
El elemento constitutivo fundamental del universo es ya un sistema. De acuerdo con el principio de Zeilinger, un sistema elemental contiene un bit de información.
-
La entropía es una medida de la información que sale (output) de un sistema al descomponerse éste en sus subsistemas constitutivos. De igual forma, la llamada neguentropía, es una medida de la información que fluye del exterior hacia el sistema (input) y que se requiere para que continúe funcionando como tal.
-
Un sistema, para aceptar información adicional debe incrementar su complejidad, es decir aumentar sus elementos y consecuentemente las interacciones entre ellos. Así, un quark, es ya un sistema complejo con una cantidad de información que no puede aumentarse.
-
Los agujeros negros son sistemas que descomponen la energía-materia en sistemas elementales
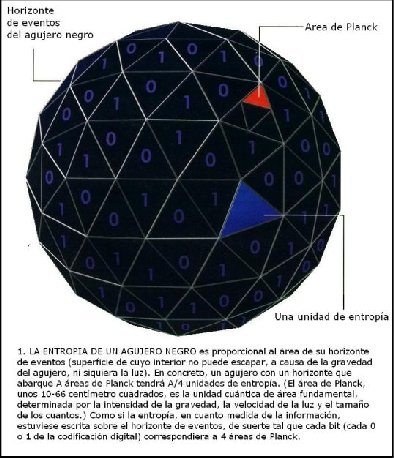
(Figura 1)
(Tomado de Scientific American Latinoamérica. La Información en el Universo Holográfico. Jacob D. Bekenstein. Año 2 No. 15 octubre de 2003)
Febrero 2007
(NOTA 1) Comentarios al artículo La Información en el Universo Holográfico. Jacob D. Bekenstein. Scientific American Latinoamérica Año 2 No. 15 octubre de 2003
[al texto]
(NOTA 2) Ibid.
[al texto]
(NOTA 3) SCHWARTZ, M. D., y Sharon Begley. The Mind and the Brain. Neuroplasticity and the power of Mental Force. Harper Collins. New York. 2002.
[al texto]
(NOTA 4) SUSSKIND, Leonard, Black Holes and the Information Paradox, Scientific American. April 1997
[al texto]
(NOTA 5) S. Hawking se ha retractado de esta afirmación (nota de la versión revisada en 2006)
[al texto]
